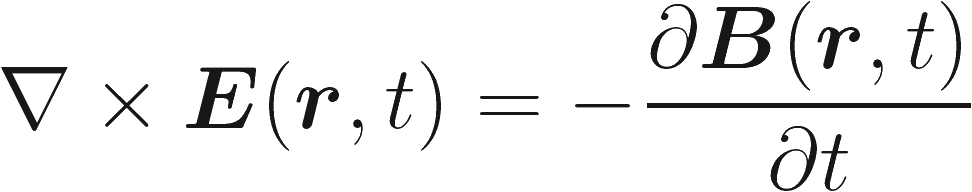 ,
,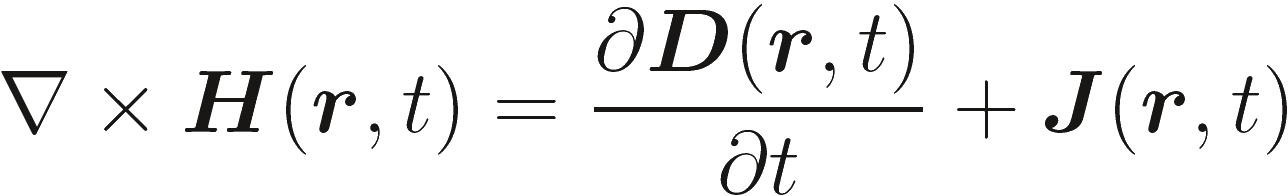 ,
, ,
,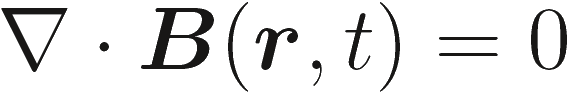 ,
,Цель этой главы состоит в том, чтобы ввести соответствующие уравнения для вычисления электромагнитных полей и их изображений цепи в едином систематической форме. Как известно, Уравнения Максвелла обеспечивают основные уравнения, управляющие электромагнитными полями если дополнены основными отношениями, имеющими отношение к средам на рассмотрении и их соответствующими граничными условиями. Эти уравнения являются подходящими для того, чтобы применить числовое/аналитическое решение данной задачи.
Имея дело с Уравнениями Максвелла мы подчеркнем формулировку Лапласа (s-домен) , у которой есть несколько преимуществ. Во-первых, решения s-домена в цифровой форме эффективны, потому что, как только решение вычислено, качания частоты и переходное исследование также выполнимы со скромным числовым усилием. Во-вторых, решения s-домена - хорошо подходят для преобразования в эквивалентные цепи; эти эквивалентные цепи могут быть объединены с ускоряющим напряжением и текущими источниками, и все устройство может быть смоделировано при использовании моделирующих устройств цепи. В-третьих, электромагнитное исследование может быть выполнено или при использовании дифференциала - или при использовании методов интегрального уравнения. Кроме того, есть преимущество выражения системы уравнений в формате, который распространен в теории линейных устройств. Формат является таким, который позволяет нам идентифицировать параметры состояния устройства, источников, наблюдаемых количеств и всех соответствующих передаточных функций. Этот метод также выдвигает на первый план проблемы относительно единственности решения, возможности выражения режима устройства с минимальным объемом данных, и стратегии применений моделей приведенного порядка.
В этой главе мы будем иметь дело с абстрактными модэлями, где электромагнитные поля изменяются в пространственно-временном континууме, то есть в системе с бесконечным размером. Этот формализм может быть приспособлен в более поздних главах к дискретности и процессам усечения в конечных измерениях, делая эти устройства, подходящие для числовых вычислений.
Уравнения, связывающие количества электромагнитного поля, были представлены Максвеллом Джеймсом Клерком в элегантном трактате, сначала изданном в 1873, и затем включили в [1] (см. также [2] для большей исторической информации). Мы предположим, что студент, читающий книгу, знаком с этими уравнениями, которые обычно представляются в предварительных курсах, и что у него или нее есть общие знания о соответствующих экспериментальных фактах и их теоретической интерпретации. В дальнейшем, мы получим Уравнения Максвелла для изменяющихся во времени частоты и доменов ( s ) Лапласа.
Это общепринято, чтобы написать Уравнения Максвелла или в локальном или в глобальной форме; мы сначала рассмотрим их локальную форму. Мы также отмечаем, что, к сожалению, это общепринято, чтобы определять локальную форму как дифференциальную форму, и это производит некоторый беспорядок с общим подразумевать, что дифференциальные формы имеют. В следующем этой книги, так как не используются дифференциальные формы, двусмысленность решена.
В трехмерной векторной системе обозначений, с вектором r указание на положение в пространстве и t переменная времени, Уравнения Максвелла
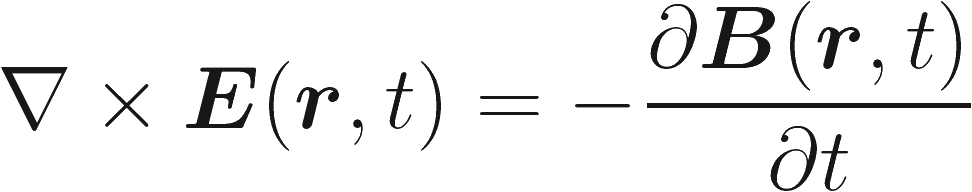 , , |
Закон Фарадея | (2.1a) |
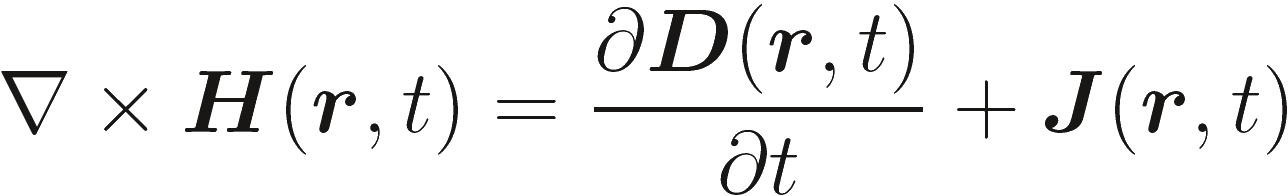 , , |
Закон Ампера | (2.1b) |
 , , |
Закон Гаусса | (2.1c) |
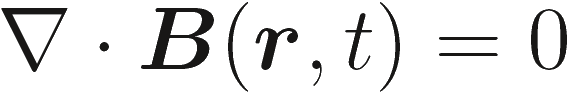 , , |
Неразрывность магнитного потока | (2.1d) |
где жирным шрифтом обозначены векторные величины. Количества - определены как
| E(r,t) | напряженность электрического поля |
| D(r,t) | электрическая индукция |
| B(r,t) | магнитная индукция |
| H(r,t) | напряженность магнитного поля |
| J(r,t) | плотность электрического тока |
| re(r,t) | плотность электрического заряда |
Уравнения (2.1a) - (2.1d) не являются независимыми, поскольку, например, мы можем получить (2.1d), взяв дивергенцию (2.1a).
Другое фундаментальное соотношение можно получить, применяя операцию дивергенци к (2.1b) и используя (2.1c)
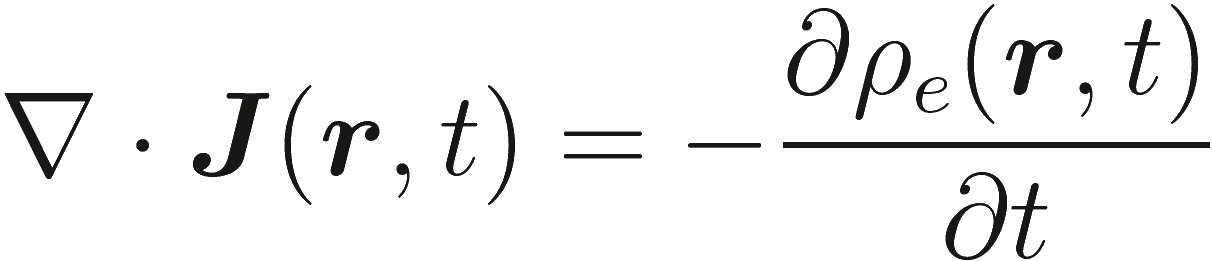 |
(2.2) |
которое описывает закон сохранения электрического заряда и плотности тока. (уравнение непрерывности)
Фактически, множество трех уравнений (2.1a), (2.1b) и (2.2) можно рассмотреть как независимые уравнения, описывающие макроскопические электромагнитные поля, так как два уравнения Гаусса (2.1c) и (2.1d) могут быть получены из этого множества. Отметим, что в стационарном случае ∂/∂t = 0 электрические и магнитные поля не являются больше взаимозависимыми, и уравнения (2.1a) - (2.1d) становятся
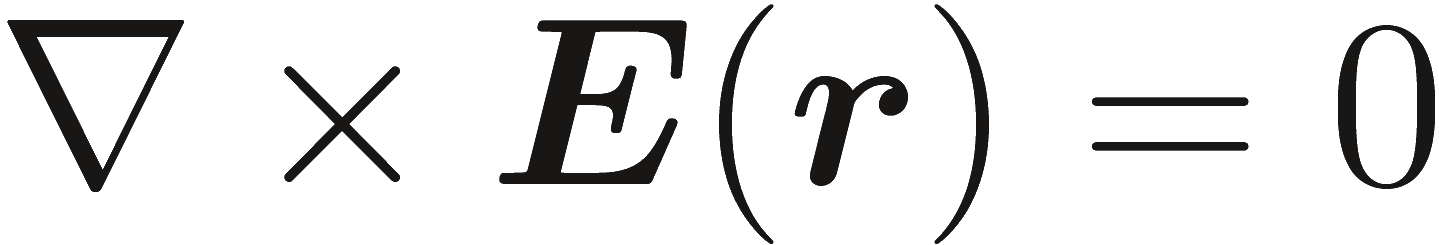 |
(2.3a) |
 |
(2.3b) |
 |
(2.3c) |
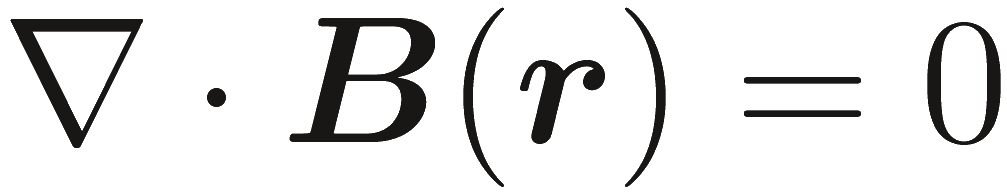 |
(2.3d) |
Наконец также отметим, что, если мы задаем плотность
электрического тока J(r) и
плотность электрического заряда re(r), мы
имеем, от (2.1a) и (2.1b), два векторных уравнения (то есть шесть
скалярных уравнений), в то время как у нас есть четыре неизвестных
вектора (то есть двенадцать скаляров). Для полного числа мы должны
учитывать свойства среды, выраженные уравнениями.
Свойства электромагнитного поля могут также быть выражены глобально эквивалентной системой интегральных отношений путем использования двух фундаментальных теорем векторного анализа: теорема Остроградского о дивергенции и теорема Стокса [3].
Дивергенция или Теорема Гаусса
Пусть U(r) любая вектор-функция положения, непрерывна вместе с ее первой производной всюду по объему V ограниченному поверхностью S. Теорема Остроградского о дивергенции гласит
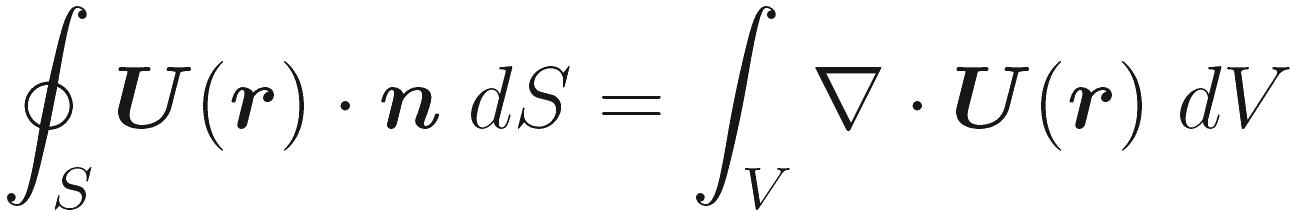 |
(2.4) |
где n - единичный вектор направленный наружу по нормали к S. Фактически, теорема Гаусса может также использоваться для определения дивергенции.
Теорема Стокса
Пусть U(r) любая вектор-функция положения, непрерывна вместе с ее первой производной всюду по произвольной поверхности S ограниченной контуром C, и считается разрешимой в конечное число обычных кривых. Теорема стокса (также названный теоремой ротора) гласит
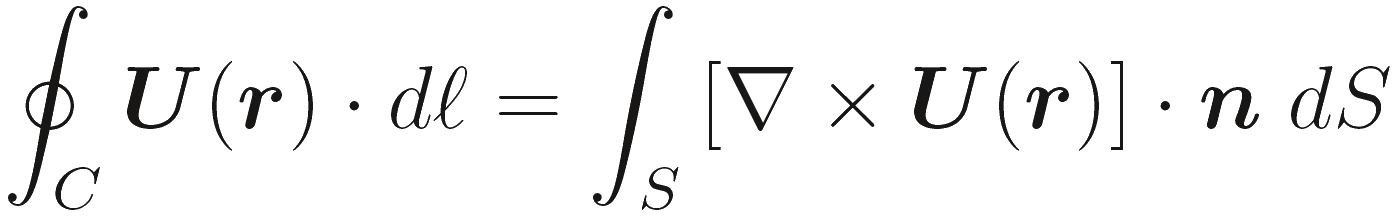 |
(2.5) |
Применяя операцию ротора для (2,1a) и (2.1b), и дивергенцию для (2.1c) и (2.1d), получаем
 |
(2.6a) |
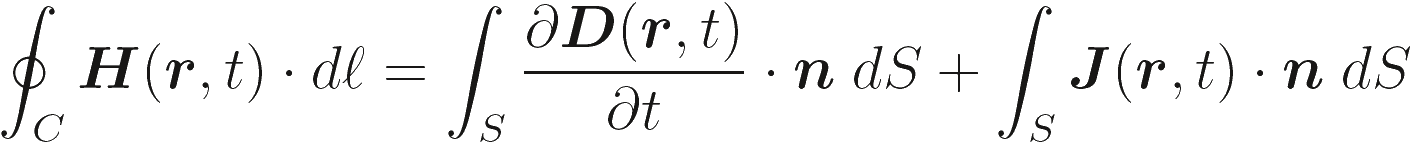 |
(2.6b) |
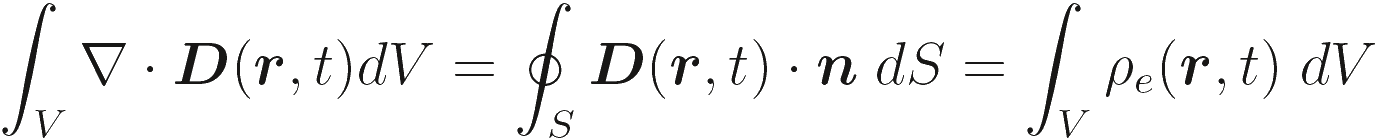 |
(2.6c) |
 |
(2.6d) |
Определяя ток I(t) как
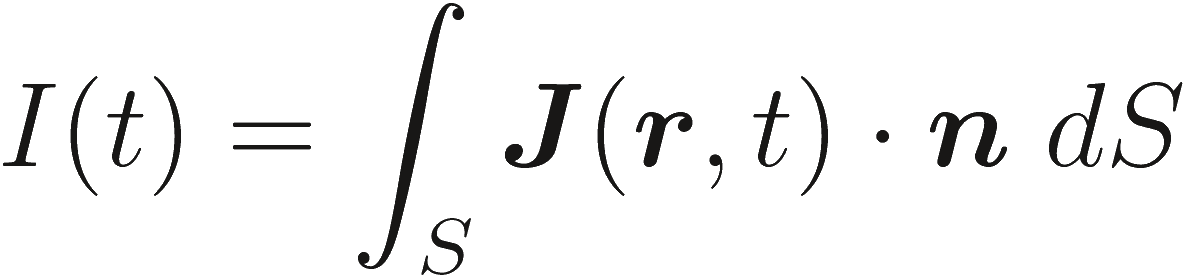 |
(2.7) |
заряд Q(t) как
 |
(2.8) |
и поток магнитной индукции как
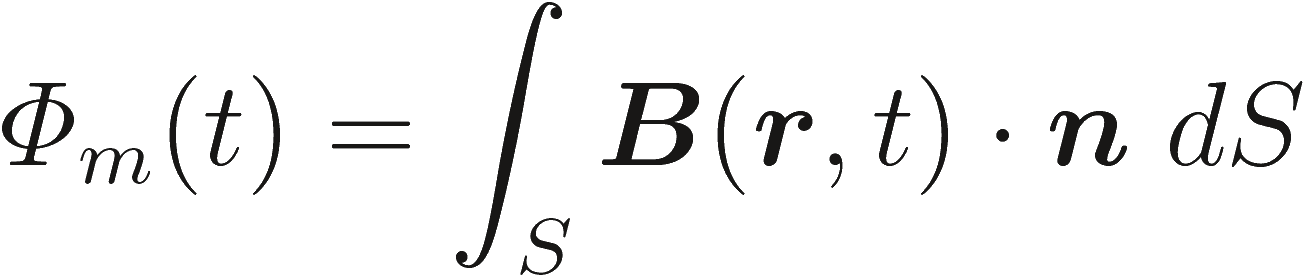 |
(2.9) |
мы можем переписать предыдущие уравнения как
 |
(2.10a) |
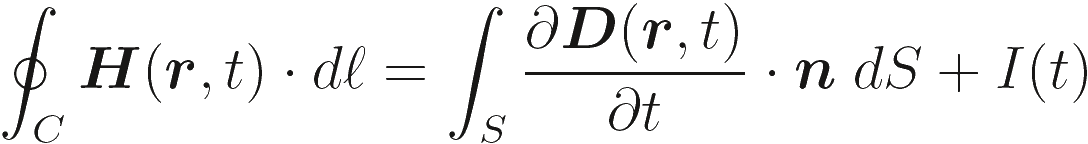 |
(2.10b) |
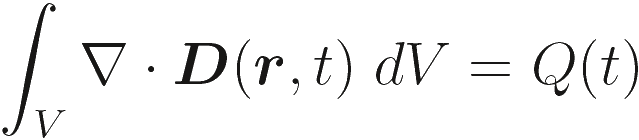 |
(2.10c) |
Электромагнитные поля, работающие на определенной частоте, известны как время гармонической стационарной или монохроматических полей. Приняв ejωt как зависимость поля от времени, чтобы обозначить время гармоникого поля с угловой частотой ω, запишем
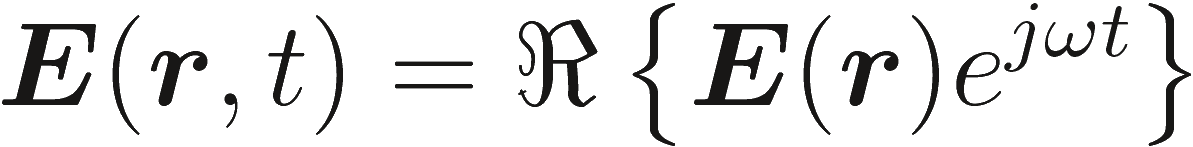 |
(2.11) |
где ℜ обозначает математический оператор, который выбирает действительную часть комплексной величины. Комплексная величина Е(r) называется фазовый вектор. В (2.11) мы использовали тот же символ для обозначения реальной количественной величины в домене от времени, E(r,T), а Е(r) комплексная величина в частотной области. В дальнейшем мы будем использовать комплексные величины, если явно не указано иное.
Используя (2.11) для величин, входящих в (2.1а), (2.1b), (2.1c) и (2.1d) получим уравнения Максвелла в частотной области. В качестве примера рассмотрим (2.1), получаем
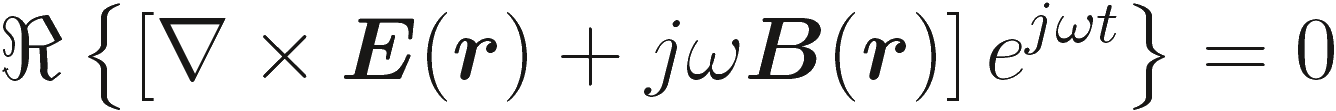 |
(2.12) |
Так как это уравнение справедливо для всех t, мы используя лемму можем утверждать, что величина в квадратных скобках должна быть равна нулю. Применяя те же рассуждения и для уравнений (2.1b), (2.1c) и (2.1d) получаем.
 |
(2.13a) |
 |
(2.13b) |
 |
(2.13c) |
 |
(2.13d) |
В дальнейшем, мы используя эквивалентность теоремы, введем магнитный поток, М(r), и плотность магнитного заряда, ρm(r). Эти величины, хотя и не присутствует физических определения, помогут в решении некоторых краевых задач.При рассмотрении и магнитных токов и зарядов, в частотной области уравнения Максвелла становятся
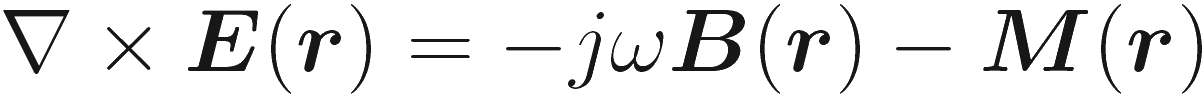 |
(2.14a) |
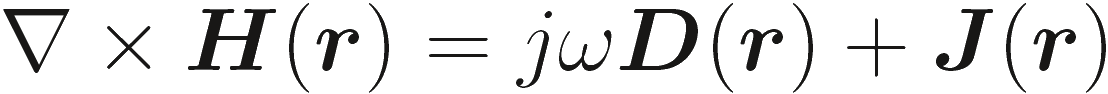 |
(2.14b) |
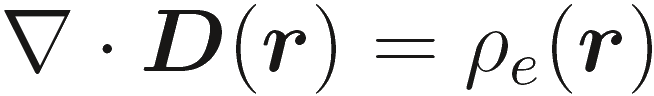 |
(2.14c) |
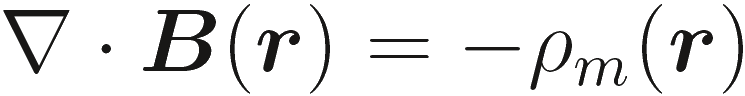 |
(2.14d) |
Вводя комплексную переменную s = σ + jω, преобразование Лапласа определяется обычно как
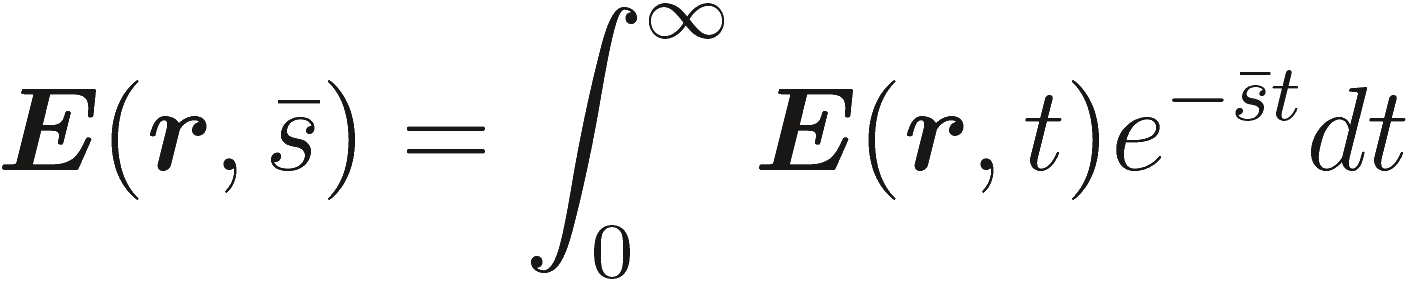 |
(2.15) |
В (2,15) мы использовали символ для обозначения такой же как количество в домене времени, E(r,t), и что в S-области, E(r,s). В дальнейшем мы будем все относяшееся к этим величинам без явного выставке s или t зависимость, причем последняя ясна из контекста.
Применяя (2.15) в для величин, входящих в (2.1а), (2.1b), (2.1c) и (2.1d) получаем уравнения Максвелла для s-домена
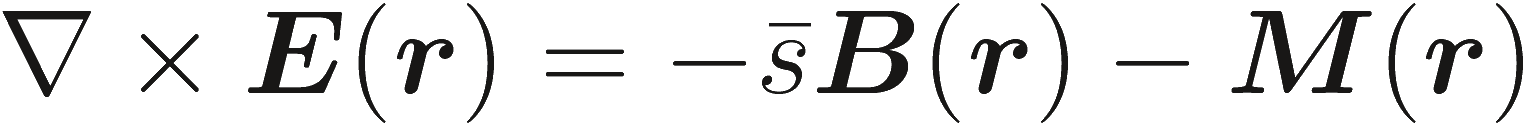 |
(2.16a) |
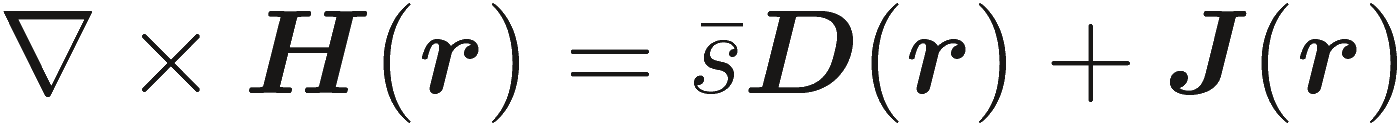 |
(2.16b) |
 |
(2.16c) |
 |
(2.16d) |
Как уже отмечалось уравнения Максвелла не могут быть решены, если отношения между векторов поля D и B с E и H определены. Тип поля, создаваемого данным источником зависит от характеристик среды, которые могут быть определены как
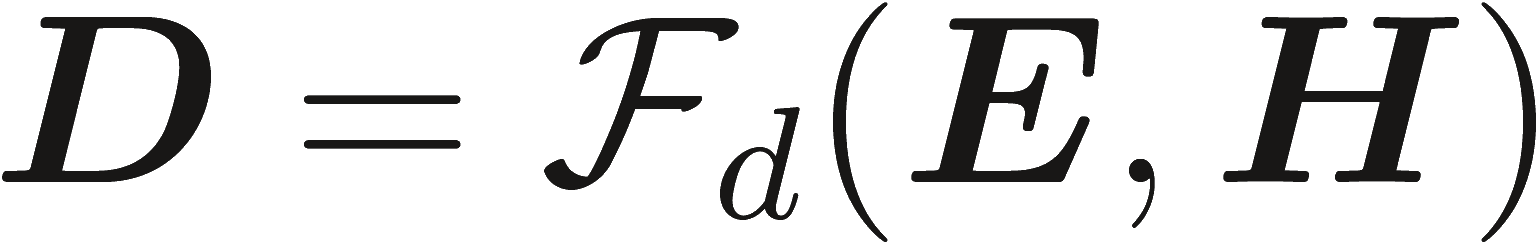 |
(2.17a) |
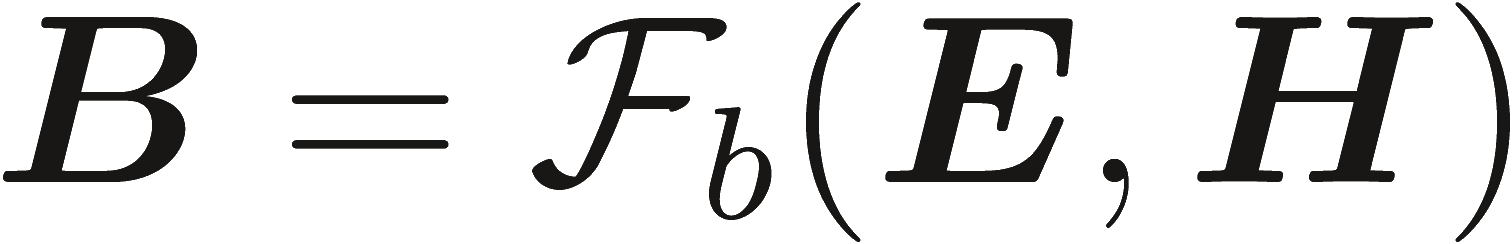 |
(2.17b) |
Здесь, Fd и Fd соответствующие функционалы зависящие от среды
считаются;
они могут быть классифицированы как:
Мы будем иметь дело только с линейной, стационарной средой, однако, неоднородные среды включены из-за их практического значения.
Другое свойство среды осуществляет векторную форму определяющих соотношений. Простейшии случай при рассмотрении изотропных сред, где определяющие соотношения имеют вид
 |
(2.18a) |
 |
(2.18b) |
где ε обозначая диэлектрическая проницаемость и μ магнитная проницаемость. В этом случае E параллельно D и B параллельно H. В частности, в свободном пространстве, уравнения переписываются с помощью материальных параметров вакуума, т.е. ε0 диэлектрической и μ0 магнитной проницаемости, как
 |
(2.19a) |
 |
(2.19b) |
где
 |
(2.20a) |
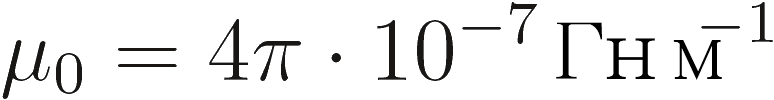 |
(2.20b) |
 |
(2.21a) |
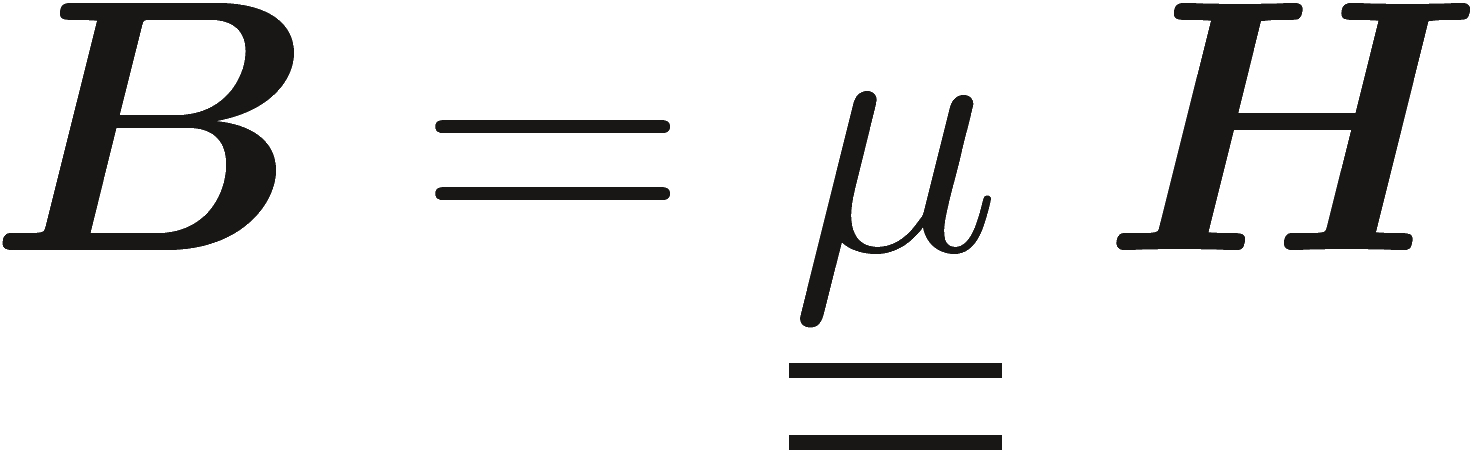 |
(2.21b) |
где μ является тензором магнитной проницаемости и ε является тензором диэлектрической проницаемости. Среда называется электрически анизотропной, если она описывается тензором диэлектрической проницаемости ε и магнитно анизотропной, когда она описывается тензором магнитной проницаемости μ. Среда может быть как электрически так магнитно анизотропной. Интересный частный случай, что двухосных кристаллах, которые могут быть описаны, выбирая подходящие частности системе координат, так называемый основной системы, в терминах тензора типа:
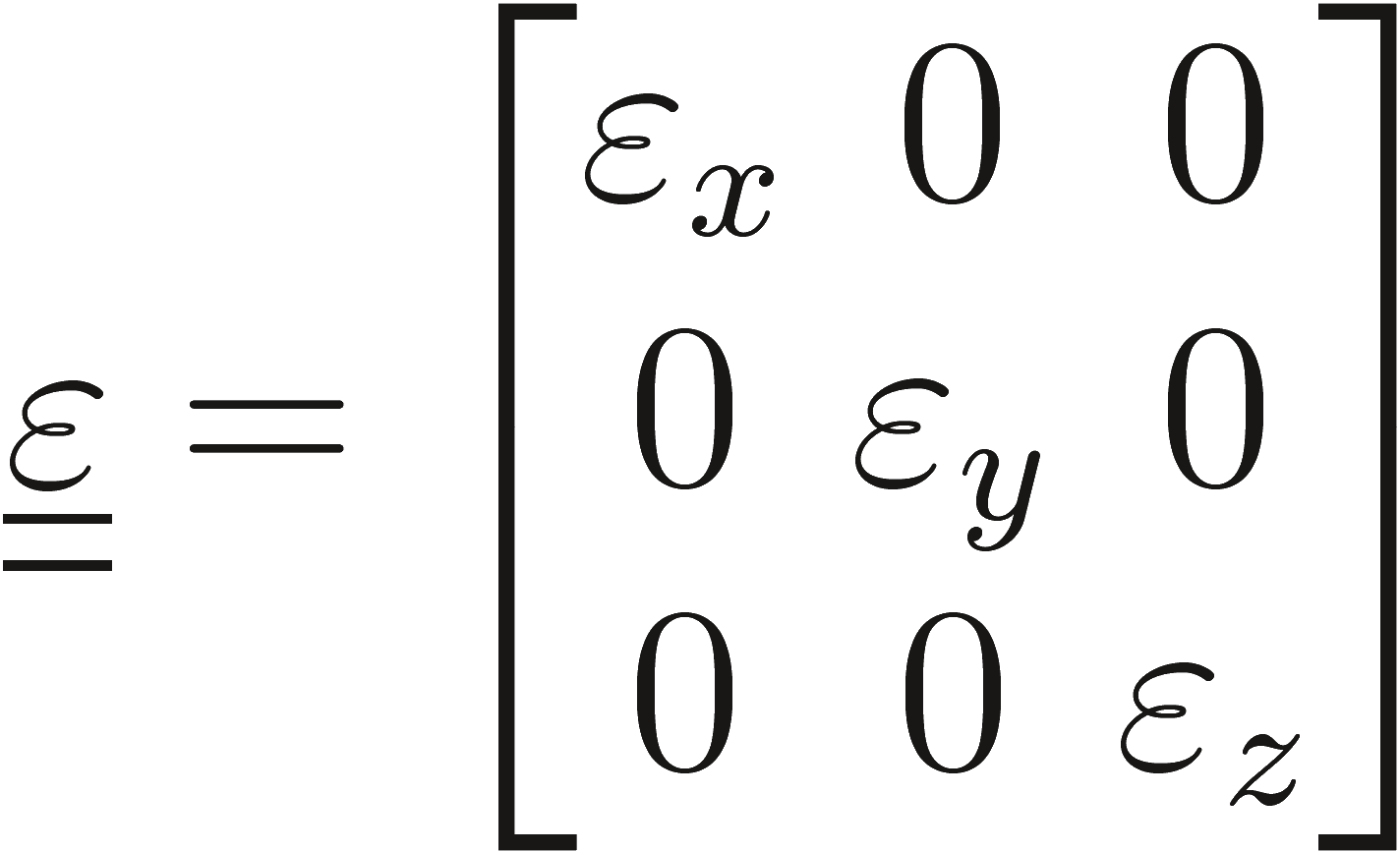 |
(2.22) |
Кубические кристаллы, где εх = εy = εz, изотропны; тетрагональной, гексагональной и ромбоэдрической кристаллы имеют два параметра равные и среда называется одноосной. Главная ось которая проявляется как анизотропия также называется оптической осью. Когда все три параметра различны, как в ромбических кристаллах, среда называется двухосной.
Когда среда имеет элементы, обладающие постоянным электрических и магнитных диполем вдоль или навстречу друг другу, приложенное электрическое поле одновременно выравнивает электрические и магнитные диполи, аналогично, приложенное магнитное поле, которое выравнивает магнитные диполе одновременно выравнивает и электрические диполи [4,с.8]. Для описания таких сред Теллеген, в 1948 году, введен новый элемент, Гиратор, в дополнение к резистору, конденсатору, индуктору и идеальному трансформатору. Эта среда, при помещении в электрическое поле, или магнитное поле, становится как поляризована так и намагниченна, и они называется бианизотропная, и которое характеризуется соотношениями типа
 |
(2.23a) |
 |
(2.23b) |
Примерами гипотетических материалов, в которых непосредственно связаны электрические и магнитные поля являются идеальным электромагнитными проводниками (PEMCs), которые были обсуждены Сихвола и Линделл [5]. В PEMC электрические и магнитные поля на уровне чувствительности материала и приводит к электрической и магнитной поляризаций, однако отклик среды не чувствителен к ориентации вектора электрического и магнитного поля. P. Russer ввела теоретическую модель для поля гиратора и схему теоретических граничных условий своиств гиратора [6].
Для того чтобы получить единственное решение уравнений Максвелла для поля, нужно ввести соответствующие границы, излучение, и краевые условия. Излучение и краевые условия представить в форме, соответственно, исходящих волн необходимое условие для поля в бесконечности возбужденных источников, в ограниченной области и сохранение энергии в сингулярных полях, создаваемых в непосредственной близости от края и угла (конца) на препятствии рассеивателями. Эти условия обсуждались обычно используятся поле решений волнового уравнения в координатной системе, и они рассматриваются ниже в разделе VII. Мы будем иметь дело здесь только с граничными условиями, возникающих на границе раздела между двумя различными средами.
Рассмотрим регулярную поверхность S на границе среды , как показано на рисунке 2.1, где индексы 1 и 2 различют величины в областях 1 и 2, соответственно.Из (2.6а) и (2.6b), как следствие предельного перехода, получаем следующие уравнения:
 |
(2.24a) |
 |
(2.24b) |
где J и M, соответственно, электрические и магнитные поверхности текущего распределения плотности на границе раздела. Аналогично, из (2.6c) и (2.6d), для малого объема на границе, предельный способ дает,
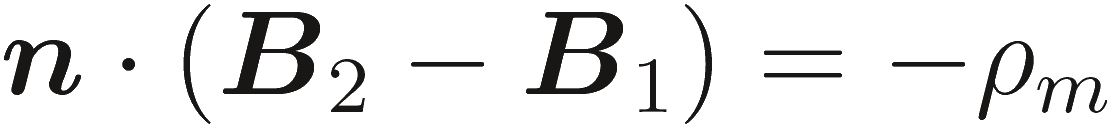 |
(2.25a) |
 |
(2.25b) |
где ρm и ρe являются, соответственно, электрической и магнитной поверхностой плотностью зарядов распределеных на поверхности.
Если ни одна среда не является идеально проводящей, тангенциальная составляющая поля Е и Н являются непрерывными, а их нормальные компоненты испытывают скачок из-за разрыва в диэлектрической и магнитной проницаемости
Когда среда 1 является идеальным проводником , поле внутри среды равно нулю и индуцированные электрические заряды и токи существуют на поверхности. В этом случае мы имеем:
 |
(2.26a) |
 |
(2.26b) |
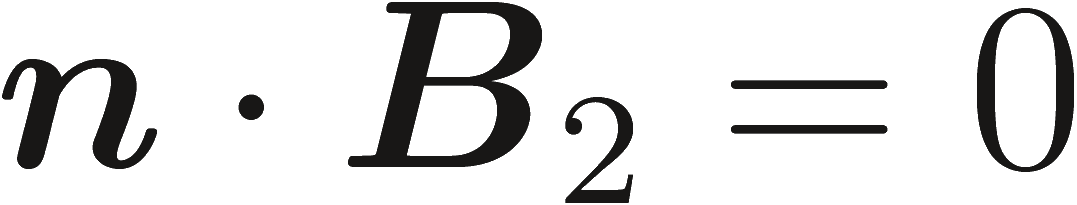 |
(2.26с) |
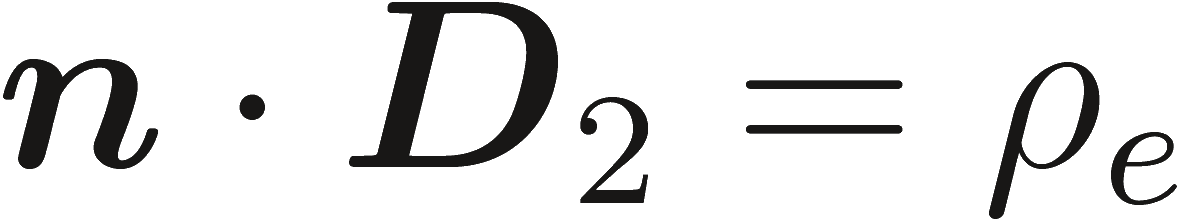 |
(2.26d) |
в котором говорится,о исчезающих на поверхности металла, тангенциальной компоненты Е и нормальной составляющей H.
В некоторых случаях это удобно включив поля, создавающие эквивалентные магнитные токи. Соответственно, поле, создаваемое магнитным распределения тока в непосредственной близости от прекрасно (электрически) проводящей поверхности определяется
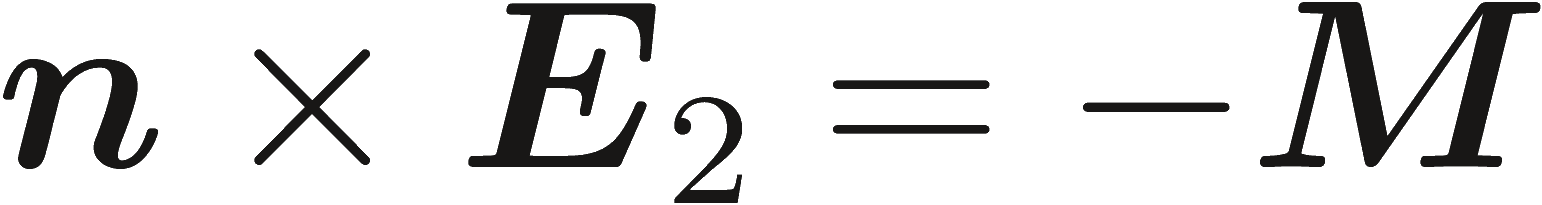 |
(2.27) |
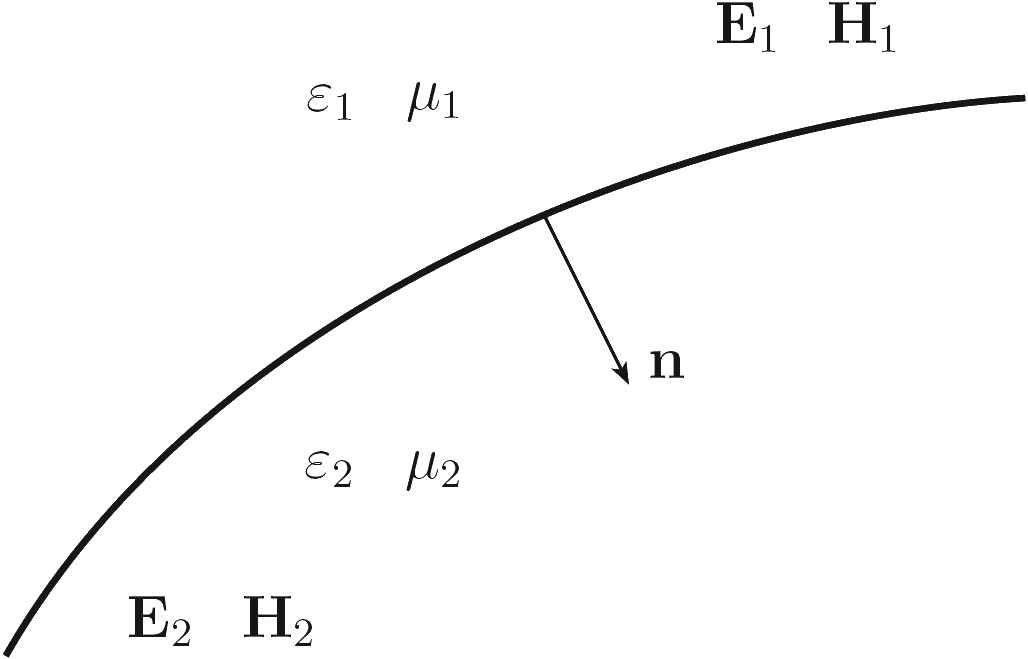 |
| Рис. 2.1. Границы раздела двух сред. |